A Harmonic Balance Approach for Designing Compliant Mechanical Systems with Nonlinear Periodic Motions
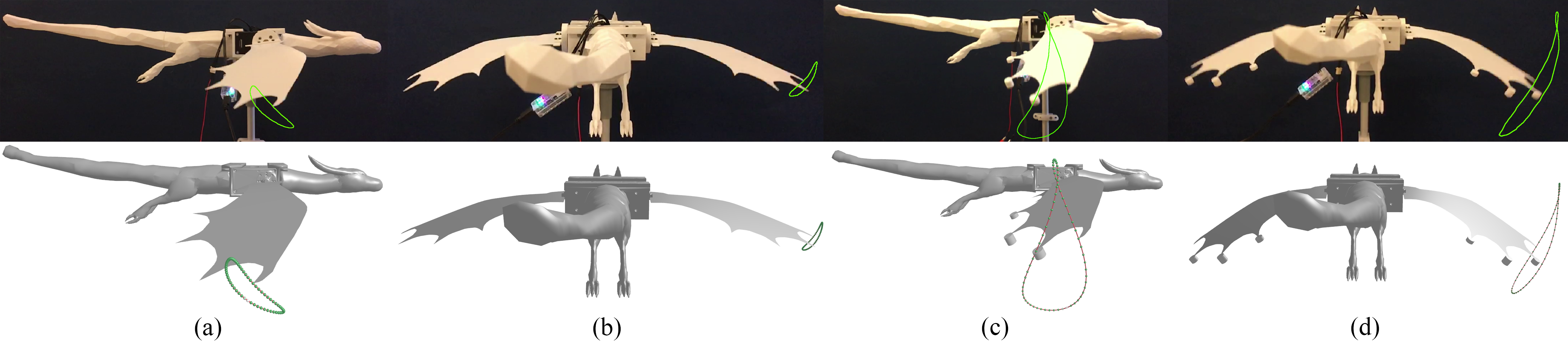
Fig. 1. Our method enables optimization-driven design of compliant mechanical systems with periodic large-amplitude motions. For this pair of dragon wings, the initial design (a, b) exhibits only small oscillation response when driven by harmonic forcing at a frequency of 2.5Hz. Our approach automatically finds optimized design parameters (extra masses at the trailing edge of the wing) that lead to substantially increased amplitude (c, d).
Abstract
We present a computational method for designing compliant mechanical systems that exhibit large-amplitude oscillations. The technical core of our approach is an optimization-driven design tool that combines sensitivity analysis for optimization with the Harmonic Balance Method for simulation. By establishing dynamic force equilibrium in the frequency domain, our formulation avoids the major limitations of existing alternatives: it handles nonlinear forces, side-steps any transient process, and automatically produces periodic solutions. We introduce design objectives for amplitude optimization and trajectory matching that enable intuitive high-level authoring of large-amplitude motions. Our method can be applied to many types of mechanical systems, which we demonstrate through a set of examples involving compliant mechanisms, flexible rod networks, elastic thin shell models, and multi-material solids. We further validate our approach by manufacturing and evaluating several physical prototypes.Materials
Results




Fig. 9. Running Ostrich. Four images from a running sequence of our ostrich model with two legs driven at 1.2Hz with a phase offset of half a period.
